引言
从大一开始,我就一直在尝试解决这个问题:选课时投的豆子(意愿值)背后是否存在数学规律?
刚进工大时,我们新生对怎样投豆、投多少豆完全没有经验。当时有学长分享了个大致规则,也就是多少k值(预选课人数/课程容量)一般会投多少豆子,比如k=1.3时大概投20个豆,本文暂且将此经验法则命名为k-豆曲线$d=f(k)$。经过几次选课后,我总结以下的经验规则:
- 越高的k对应越高的豆子。
- k-豆曲线存在边际递减效应。
因此在大一下的选课时,我就用对数函数来拟合这种规则了,但这个法则有数学定理支持吗?
基本假设
我大一时对该问题的建模和初步想法在现在看来,实际上是非常散乱的,这很大程度上是没有首先确定好简单、合理的假设所导致的。最近趁着考试周空闲的时间,我慢慢对该建模问题及其假设有了初步的想法。
为了大幅简化问题,我们设想以下情景:一个学校有m个课程可供n位学生选择,每个学生有100个豆子,每个课程的容量都为v,已知每门课程的预选课人数$e_i$,试探究k-豆曲线等可能存在的数学规律。
显然豆子的数量不影响我们对结论的进一步探索,不失一般性设为100个。m、n和t都应该对结果有影响(准确来说应该是它们的相对比值)。此外,预选课人数e也会对结果产生影响。
我们首先提出一个关于理性人的假设:
假设1:对任意两个选课课表相同的学生,他们对同一门课所投的豆子都是一样的。
该假设的关键在于回答“意愿值由什么决定”的问题。个人认为“意愿值”名字本身比较容易误导人,似乎在表明该数值是与人的意愿呈正比的,但是从经验来讲,一门课的意愿值很大程度上受该生所选的其他课程的k值所决定的。一个选课很少的人相比一个选课很多、基本选热门课的人,对同一门课所投的豆子显然更多。
有人可能会问,个人风险偏好难道不会影响两人所投的豆子吗?我认为在理性人的假设下,假设1的个人差异因素不会非常显著。此外,假设1的提出也明显简化了对问题的分析,在此基础上我们可以进一步提出下一个假设:
假设2:学生对自己所选课的投豆分布正比于他们各自的k-豆曲线。
通过已知的所有所选课的k值,k-豆曲线可以给出学生所投豆子的权重分布。假设学生选课集是$M$,$k_i=\frac{e_i}{v}$,那么第i个课程所投豆子为$d_i=100\frac{f(k_i)}{\sum\limits_{j\in M}f(k_j)}$。这里可以看出,k-豆曲线可以乘上任意一个常数而不改变豆子分布$d_i$,其函数值也不等于豆子、而是代表权重。假设2是关于投豆机制的一个非常简单的假设,可以方便后续的分析。
最后,理性人假设还应当蕴含另一个假设:
假设3:所有学生的k-豆曲线都是相同的。
所有理性人经过充分博弈后,会达到一个纳什均衡,这个稳定的状态应该让所有人的k-豆曲线相同。
为了进一步简化本文分析,我们还有以下假设:
假设4:每个人对所有课程的选择是相互独立的。
假设5:每位学生对所选的每门课的选课意愿一样。
建模
我们的基本方法是建立一个博弈模型,通过程序模拟来得到纳什均衡,最后分析想要的结论。
在各种变量初始化后,每轮的选课博弈如下:
- 确定每门课的(大概)预选课人数$e_i$
- 使用随机采样确定所有学生的选课列表
- 所有学生根据k-豆曲线确定投豆数目
- 计算每门课的入选豆子下限
- 根据豆子下限,计算每个学生多投和少投的loss和,更新k-豆曲线
实际应用中预选课人数可以获得,在模拟场景下需要我们自己确定。直觉上讲,越好的课人数越来越多,越雷的课人数越来越少,人数在中等程度的课占比应该比较少,整体成两极分化。因此,一门课的预选课人数/学生总数的值$\frac{e}{n}$可以看作遵循一个U形分布,可用beta分布描述$p(x)=x^{\alpha-1}(1-x)^{\beta-1}/B$。
根据假设4,一个人选择课程i的概率为$\frac{e_i}{n}$,会选择课程集合$M$的概率$p=\prod\limits_{i\in M}\frac{e_i}{n}\prod\limits_{i\notin M}1-\frac{e_i}{n}$。
k-豆曲线是未知的,为了实现更好的拟合能力,我们用一个3层MLP的神经网络来拟合。为了能让博弈稳定收敛,我们初始化时训练该网络为一个线性函数$x-1$。由于k-豆曲线与常系数无关,因此我们再添加一个归一化loss。
计算每门课的入选豆子下限时会上取整,以贴合实际情况并提高竞争性。
计算loss时,一种简单的方法是,我们只关注每位学生选课列表中的课程,计算多投和少投的值的平方和作为loss。然而这存在一个不可兼得的问题——假如某生只选了两门课,入选豆子下限分别为30、90,那么均方误差会让他两门课都选不上,而通常我们还是希望放弃过于热门的课、至少能选上课。为了解决这个问题,我们可以设计一个新的loss函数:
$loss=x,\quad\text{x>=0}$
$loss=ln(-x+1),\quad\text{x<0}$
对于少投太多的课,我们对选中它的意愿会稍微低些;对于只差一点就能选上的课,我们希望神经网络能更新快点。
结果
实验时设置学习率0.001,博弈训练轮数100次(其实10次基本上都稳定了),学生数固定1000,预选课人数分布参数$\alpha=\beta=0.8$,预选课人数e至少10人,至多1000/10=100人。下面我们探究m和v的影响,并讨论2种典型情况。
指数形k-豆曲线
条件:$m=100,v=50$。
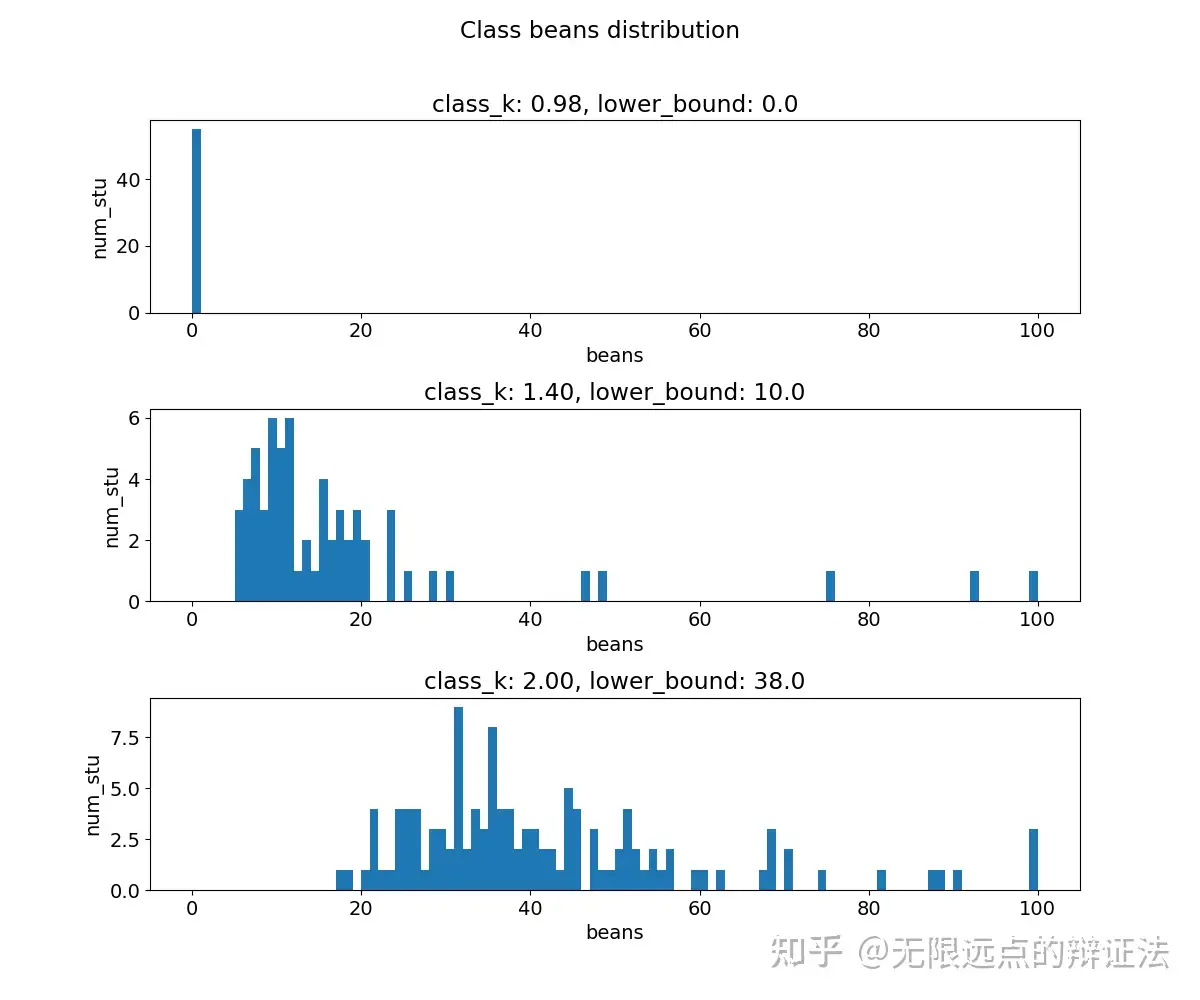
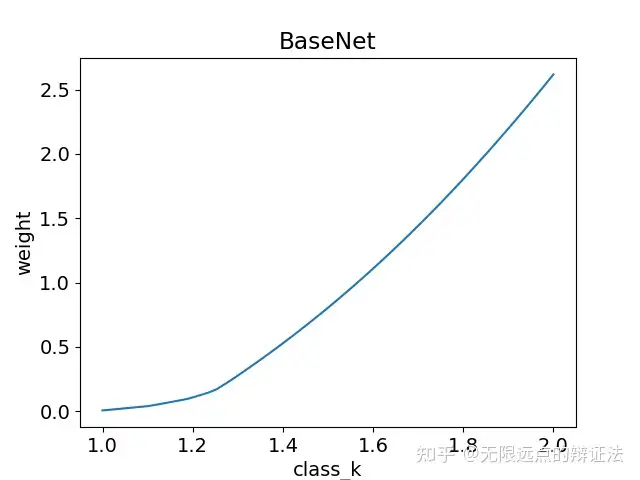
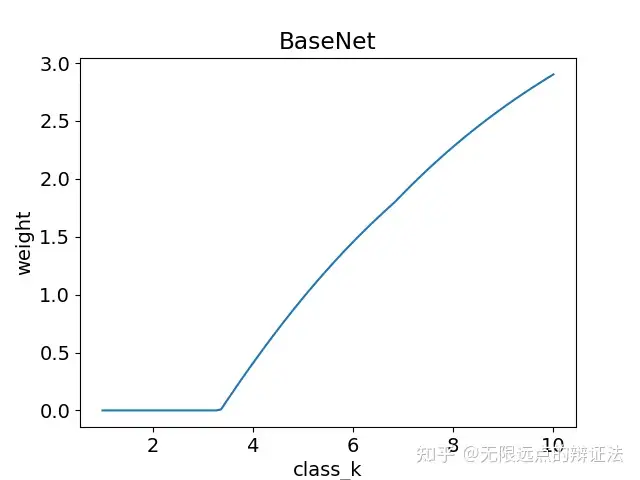
图一是中等热门、较热门、最热门的课程的投豆分布,图二是稳定后的k-豆曲线,可以看到后者大致呈一个指数增长的形态。
此时的m比较小,使得每人选课数较少,每个课的投豆数更多,导致热门课的投豆数较多、且k非常大,使得博弈过程中豆子权重不断提高,k-豆曲线变成了指数型。
直线形k-豆曲线
条件:$m=70,v=30$。
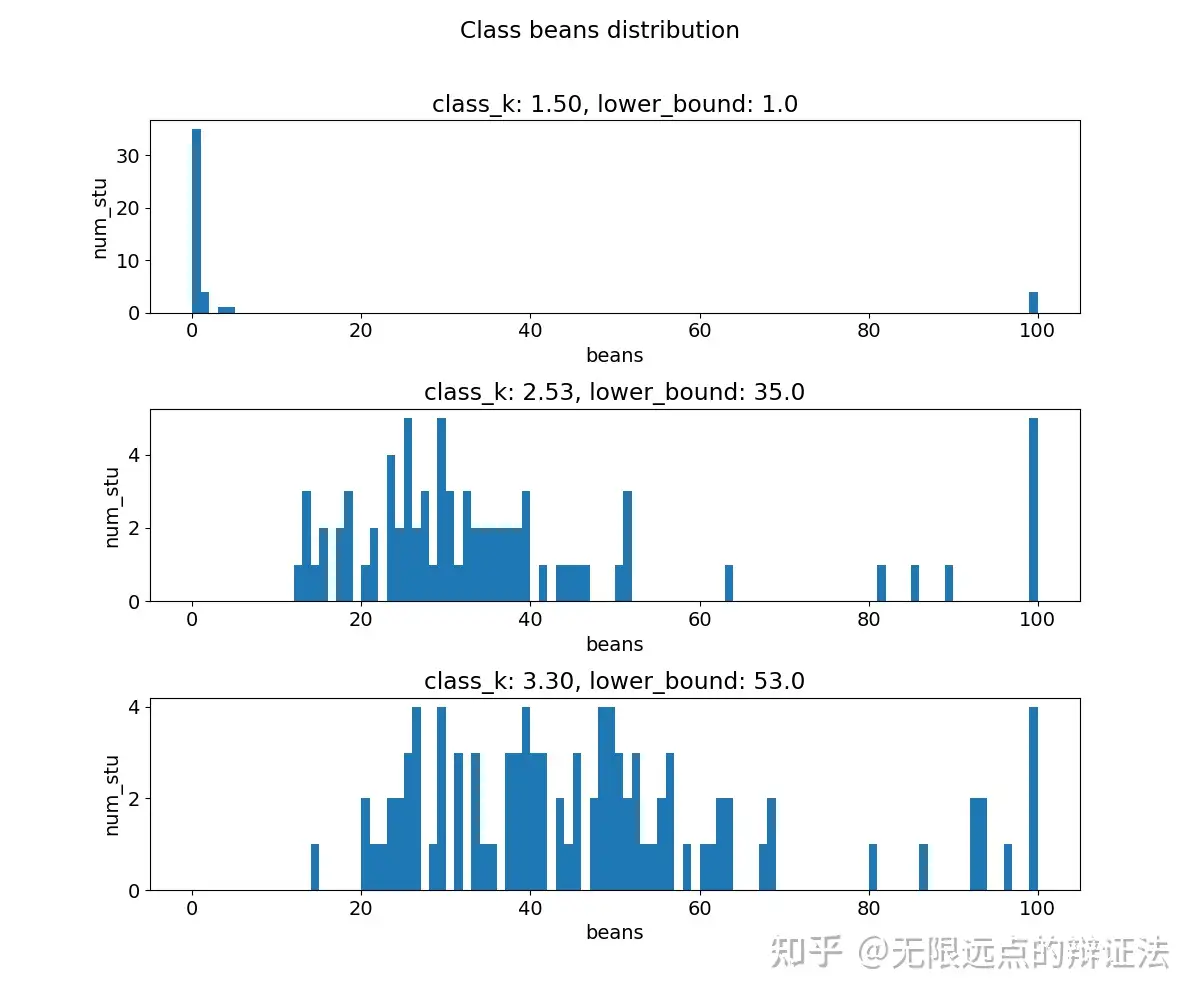
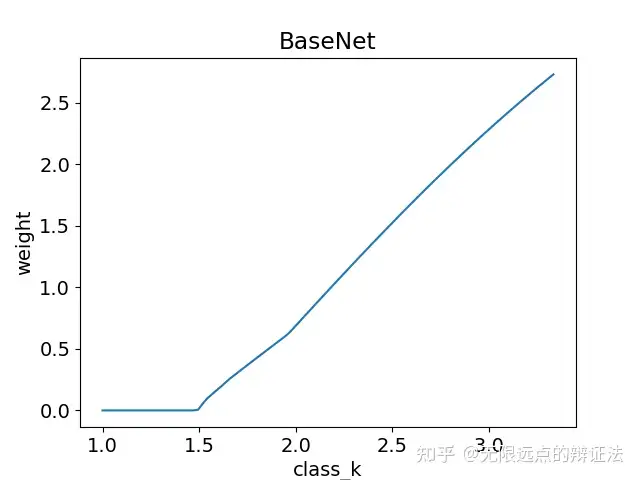
m和v都相较上面稍微减少些了,k-豆曲线现在呈一条直线。
对数形k-豆曲线
条件:$m=40,v=10$。
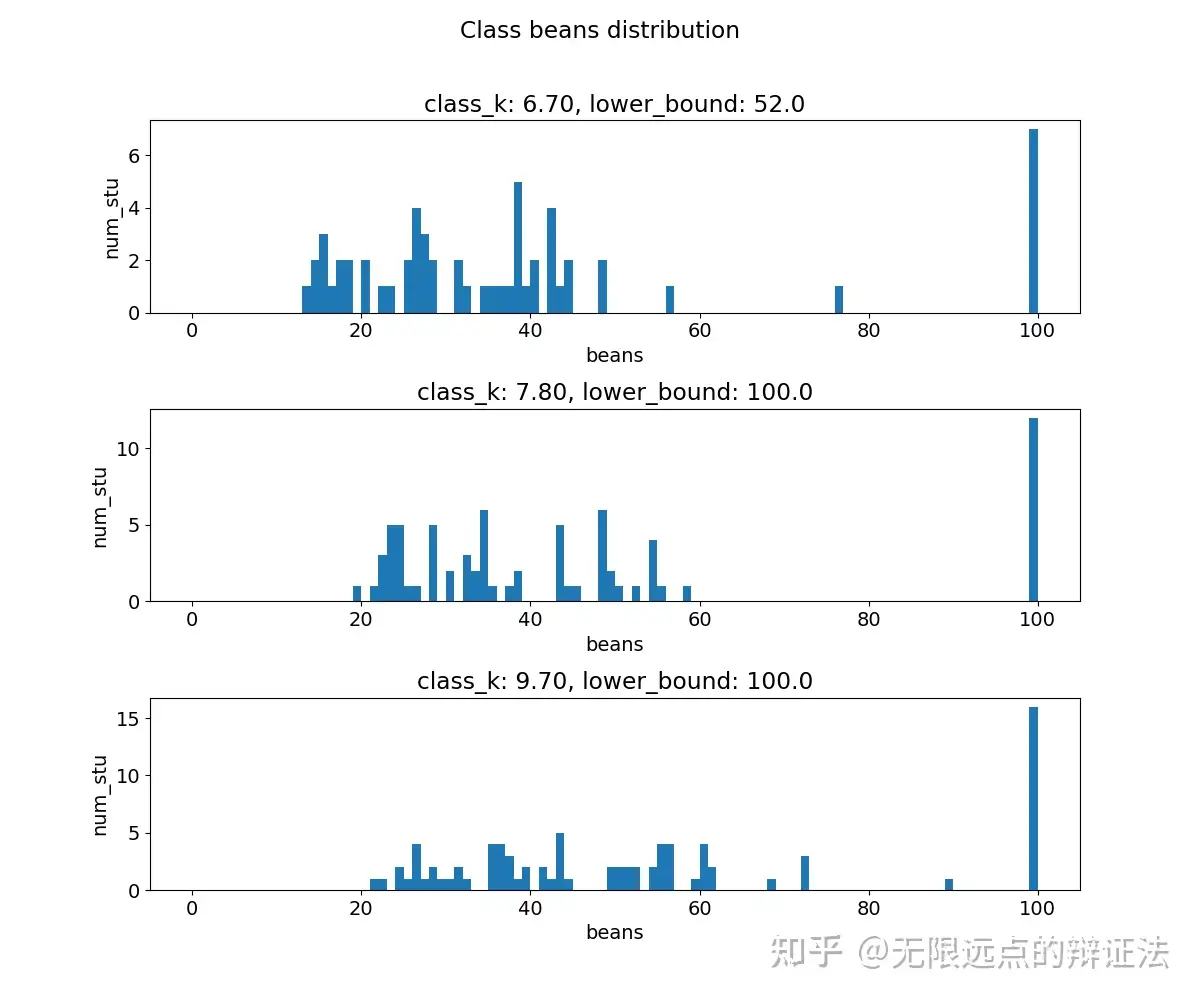
m和v都非常小,选课非常激烈,对于热门课程的投豆边际意愿递减了,导致k-豆曲线呈对数形。
最后
除了这两种情况以外,我相信应该还存在其他的k-豆曲线(例如S型),这可能需要综合调整$\alpha,\beta,m,v$等参数,因时间原因这里不继续展开。
代码开源在GitHub,感兴趣的读者可以自行魔改研究。
谨以此文献给过去的大学三年