写在前面
首先致敬神文:天文学真的对个人来说,毫无用处吗? – 鬼蝉的回答 – 知乎。
对标题中的问题感兴趣的朋友可以先去围观该答主的文章,他是这个idea的最初提出者,讲解得非常通俗易懂。而我在答主的原理基础上实现了Python的半自动化脚本,并添加了个人的一些改进,感觉非常有用(顺便写了篇论文当课程大作业,一举两得)。
我在今年寒假在知乎看到了答主的回答,他简单介绍了他所使用的方法。我觉得这个问题很有意思,当天我便尝试使用GeoGebra定位各星和灭点的位置,但由于人工直线检测过于麻烦,误差难以降低,计算过程极为繁琐,导致后来我发现自己无法解决这个问题。直到本学期我学习了数字图像处理课程,我才意识到可以使用霍夫变换等工具来检测星点和直线,从而更加精确方便地实现对单照片的定位。很快我便用Python实现了这个方法,并通过实验验证了其有效性,和朋友玩得不亦乐乎。
我的项目地址在StarPhotoPositioning,下面的内容摘自我的论文。如有瑕疵,请多指教。
摘要
照片中的天体通常能提供优质的位置信息,因而成为了航天、地理等领域的重要定位数据来源。然而,现有的照片定位方法依赖过多的信息,如拍摄角度、GPS、图片数量等,这限制了其在侦查领域的应用。本文提出一种仅基于照片中的星点与拍摄时间的定位方法,经基本的图像处理,运用天文学和几何学的推演,可实现对单照片的较高精度定位。我们首先使用霍夫圆变换检测照片中的圆形星点,精确定位其在图像中的位置,然后与拍摄时星图的匹配,计算照片焦距。我们还使用LSD算法与霍夫直线变换检测照片中的铅垂线,计算照片灭点,进而计算出各星天顶角,最终得到照片的地理位置。实验证明了我们方法较高的定位精度和较强的抗干扰能力,误差可低于50km。由于无需GPS等信息,我们的方法在军事、侦查等领域有着广泛的应用前景。
导言
从包含星空的照片中推测拍摄位置既是导航领域的重要研究课题,也在刑事侦查学科中具有重要价值。通常来说,为了在夜空中根据天体定位,我们需要知道拍摄时的时间、地点、拍摄角度等信息,甚至可能需要用到六分仪、GPS接收器等精密设备。然而,这些信息在实际应用中并不总是可得的,尤其是在军事、侦查等领域。其中,拍摄时间通常是可以通过照片的EXIF,或者其他相关信息推断而获取到的。因此,我们的研究关注于如何仅通过照片中的星点与拍摄时间信息,实现对单张照片的定位。
具体来说,我们首先检测照片中的星点在图像坐标系中的坐标,这是星图定位的基础。我们假设星点在照片中呈现为圆形,因此我们使用霍夫圆变换[1]检测照片人工框选区域中的星点,并将其圆心坐标作为星点的坐标。之后我们对比照片中的星点与拍摄时的星图,运用星与星之间的夹角信息,通过相机拍摄的几何原理计算照片的焦距。
然后,我们需要检测照片灭点在图像坐标系中的坐标,这是计算星天顶角的基础。我们使用LSD算法[2]检测照片中的直线,然后使用霍夫直线变换[1]过滤出长直线,计算其交点作为照片灭点的坐标。为了进一步滤除伪铅垂线,我们在程序中提供了直线角度的过滤区间参数。考虑到灭点容易受到干扰影响,我们还结合了人工估计的灭点坐标值,通过迭代优化的方法计算出最终的灭点坐标。
最后,我们通过灭点、星点坐标和焦距,计算各星天顶角。通过天文学和地理学知识,我们可以计算出照片拍摄地的经纬度信息。
- 我们提出了一种仅基于照片中的星点与拍摄时间的定位方法,无需GPS等信息,适用于军事、侦查等领域。
- 我们选用了鲁棒性较强的霍夫圆变换[1]和LSD算法[2],创造性地提出了基于迭代优化的灭点计算方法,提高了定位的抗干扰能力。
- 我们通过实际测试和灵敏度分析,证明了我们方法的较高定位精度和较强抗干扰能力。
在本文中,我们将详细介绍我们的定位方法、实验性能以及在侦查界的技术优势。通过讨论照片定位技术的相关研究和进展,我们希望为侦查领域提供一种新型实用的定位技术。
相关工作
自数码相机问世以来,图像定位一直是导航、侦查等领域的重要研究课题。现有的照片定位方法主要分为基于星点的方法、基于地标的方法、基于GPS的方法等,其中基于星点的方法以其高精度的特点受到广泛关注。然而,由于实际应用中的各种限制,如拍摄角度等关键信息的缺失,现有的照片定位方法仍然存在一定的局限性。其他方法,如基于地标的方法,虽然在一定程度上解决了这一问题,但其依赖于专家知识,且在实际应用中费时费力。因此,我们提出了一种仅基于照片中的星点与拍摄时间的定位方法,以解决现有方法的局限性。
网络照片定位技术在最近几年取得了长足的进步,由于新颖性、技术性和实用性等特点,以“网络迷踪”的解迷形式在民间广泛流传。一般认为,网络迷踪是一类仅凭一张照片及有限提示信息判断出照片拍摄具体地点的推理游戏。它可以被认为是开源情报(Open-Source Intelligence, OSINT)的一种形式,指合法地从公开和可公开获得的资源中收集数据和信息的做法。除社会工程学的方法外,网络迷踪一般通过图像搜索引擎检索地标建筑来定位,这通常需要用到谷歌地球等工具。专业人士还可以通过照片中的人文地理信息,如气候、山脉、植被等,或是航班等交通信息,来推断照片拍摄地点[3]。最近,已有一种关于仅依赖于时间与星点的照片定位技术的基础理论和人工方法被提出,并被成功验证[4]。
另一方面,边缘检测是图像处理的重要技术,可作为直线检测等算法的预处理程序。常见的边缘检测是通过二维滤波器运算实现的,如Sobel[5]、Prewitt[6]、Roberts[7]等算子。Canny算子[8]是一种流行的多级检测算法,借助高斯滤波器和双阈值连接,旨在找到最优边缘。Marr-Hildreth算子[9]基于二阶导数的边缘检测算法,借助拉普拉斯高斯算子,取得了较好的效果。
此外,图像的圆弧、直线识别方法的研究已经相当成熟。广义Hough变换[1]是一种经典的特征提取方式,通过投票实现检测圆弧、直线等任意形状,但缺点是调参较多、存在误检测等问题。LSD[2]是一种基于直线段的检测方法,通过假设检验自适应控制误差,可以有效地检测直线。EDlines[10]是一种快速、无参数的线段检测器,除误报率低外,它还有非常快的检测速度。LSM[11]是一种基于直线段的检测方法,通过对直线段的分割和合并,可以有效地检测和合并直线。另外,深度学习的直线检测算法,如LCNN[12]等算法,也实现了较好的直线检测效果。
图像定位通常需要大量的人力和试错次数,不同的环境背景阻碍了通用方法的适用性。通过挖掘直线检测、圆弧检测和边缘检测等方法,我们旨在找到最适合于图像定位的数字图像处理方法组合,结合天文学和几何学的知识,实现对单照片的高精度定位。我们相信,凭借低成本、少信息需求的特点,我们的方法将在侦查领域展示出强大的应用潜力。
方法
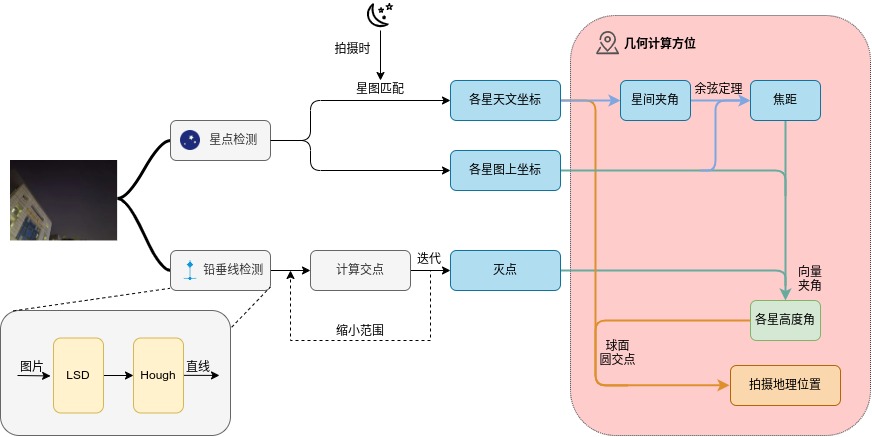
我们的方法概览如图1所示。针对一幅带有星点和铅垂线的图像,我们首先给出星点坐标(本文的坐标检测的数据都建立在opencv所使用的图像坐标系上)的检测方法,然后给出灭点坐标的检测算法,最后给出拍摄地理位置的几何计算公式。通过以上流程,我们将能实现对单照片的高精度定位。
星点坐标检测
我们假设星点在照片中呈现为圆形,因此使用霍夫圆变换[1]检测照片中的星点,并将其圆心坐标作为星点的坐标。由于图片的噪点和星点的大小不一,我们首先对图片进行高斯滤波,然后对其灰度图像使用人工框选的方式预先划定星点的范围,再通过霍夫圆变换检测[1]星点坐标。
灭点坐标检测
图像灭点是指照片中所有铅垂线的交点,因此我们首先需要检测照片中的铅垂线。虽然直线检测的方法较为成熟,但经过实验我们发现,直线检测的结果中存在大量的干扰线,这对灭点的检测造成了困难。
为此,我们首先对图像加大明暗对比度和高斯滤波处理,然后选择将两种直线检测方法结合。首先使用LSD算法[2]检测照片中的直线,然后使用霍夫直线变换[1]过滤出长直线。为了进一步滤除伪铅垂线,我们在程序中提供了直线角度的过滤区间参数,将角度在此区间的直线滤除。直线的角度计算公式如下:
$$\theta=\arctan\frac{y_2-y_1}{x_2-x_1}$$
其中,$\theta$为直线倾角,$(x1,y1),(x2,y2)$分别为直线两端点的坐标。
然而,由于照片中的干扰线较多,各种直线的交点也几乎不会重合。如果简单将所有直线的交点的平均值作为灭点坐标,将会因极值点产生较大的误差。因此,我们进一步提出了基于迭代优化的灭点计算方法。我们首先通过人工估计的方式,判断出照片的灭点坐标的粗略的估计值$(p_x^0,p_y^0)$以及估计的误差半径$R^0$。然后,从直线全集$\mathcal{L}_0$中滤除到点$(p_x^0,p_y^0)$距离大于$R^0$的直线,将距离剩下直线集$\mathcal{L}_1$距离最近的点作为新灭点估计位置$(p_x^1,p_y^1)$。我们计算新旧灭点坐标的欧氏距离,将其的1.1倍值作为新的误差半径$R^1$。重复上述过程,直到误差半径小于1个像素点或所剩直线小于2条,即可得到最终的灭点坐标。用公式表示如下:
$\mathcal{L}_{i+1}=\{l_j\in\mathcal{L}_i|dist(l_j,(p_x^i,p_y^i))\leq R^i\}$
$\underset{(p_x^{i+1},p_y^{i+1})}{\arg\min}\sum_{l_j\in\mathcal{L}_i}^{\left | \mathcal{L}_i\right |}dist(l_j,(p_x^{i+1},p_y^{i+1}))$
$R^{i+1}=1.1\sqrt{(R^i-R^{i+1})^2+(R^i-R^{i+1})^2}$
几何计算
为了计算方便和统一下文天体的坐标表示,我们首先定义一个名为标准参考系的天文坐标系,每星的坐标由标准赤经和赤纬组成。其中,标准赤经为(0°E, 0°N)的地理位置处的时角乘$-1$的值。通过拍摄时间,我们可以匹配到拍摄时的星图,从而得到各星的标准赤经和赤纬。
相机焦距计算

我们首先计算相机焦距$f$,即点$O$到照片中心的距离。根据相机原理图2,焦点始终投影在照片中心。如果我们有两个星点的图像坐标$A(x_i,y_i),B(x_j,y_j)$,以及它们在天球上的坐标$(\alpha_i,\delta_i),(\alpha_j,\delta_j)$,由球面距离公式与夹角关系可得:
$\cos\theta_{ij}=\cos\delta_i\cos\delta_j\cos(\alpha_i-\alpha_j)+\sin\delta_i\sin\delta_j$
$\cos\theta_{ij}=\frac{\overrightarrow{OA}\cdot\overrightarrow{OB}}{\left | \overrightarrow{OA} \right |\left | \overrightarrow{OB} \right |}$
$\overrightarrow{OA}=(x_i,y_i,f)$
$\overrightarrow{OB}=(x_j,y_j,f)$
其中,$\theta_{ij}$为星点$A,B$的球面距离。
对于任意两个星点,我们都可以通过求解上式的正实数解,进而得到相机焦距$f$。当存在多个星点时,我们可以通过选择所有二元星点组合,多次求解取平均值作为最终的焦距(当两个星点在图像上相距很近时,上式可能存在2个正实数解,如果图中只有这两个星点,那么将无法进行下一步计算)。为了减少误差干扰,在求均值时我们排除了$3\sigma$以外的数据。
星天顶角计算
在得到焦距$f$后,通过星点的图像坐标和代表天顶点的灭点坐标,我们可以计算出各星的天顶角,即高度角的余角。
设某一星点的图像坐标为$A(x,y)$,灭点坐标为$T(p_x,p_y)$,则该星的天顶角$\theta$可由以下公式计算:
$\theta=\arccos\frac{\overrightarrow{OA}\cdot\overrightarrow{OT}}{\left | \overrightarrow{OA} \right |\left | \overrightarrow{OT} \right |}$
$\overrightarrow{OA}=(x_i,y_i,-f)$
$\overrightarrow{OT}=(p_x,p_y,-f)$
地理位置计算
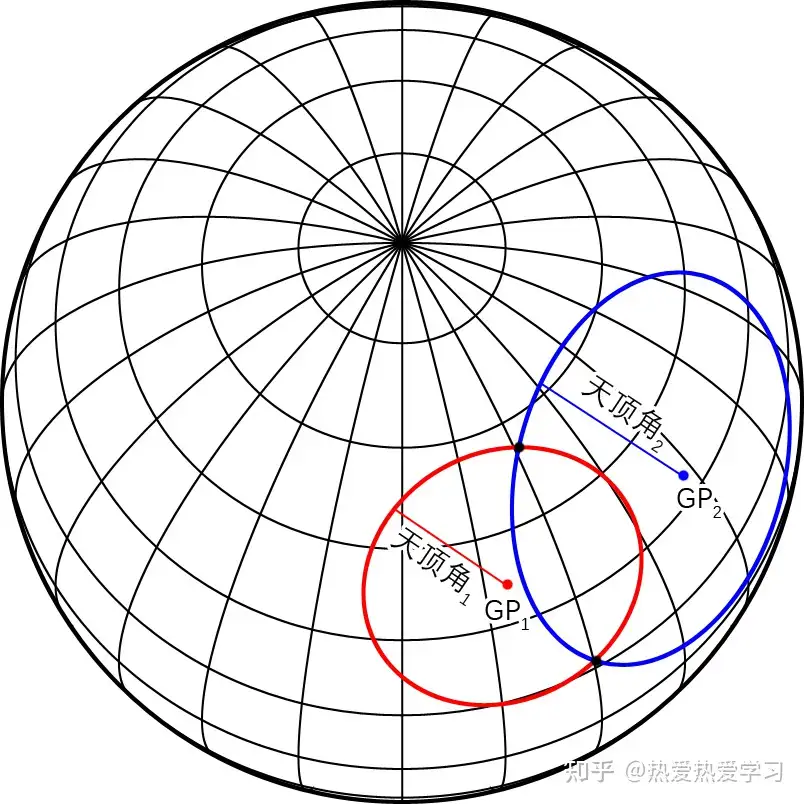
最后,我们通过天文学和几何学的知识,计算出照片的地理位置。如图3所示,已知星天顶角$\theta$和星的时角$\alpha$、赤纬$\delta$,我们可以在地球上绘制出观测该星天顶角为$\theta$的地区点集,该点集为一个天顶角半径大小的圆。显然,所有星的天顶角圆的交集即为照片拍摄地的地理位置,当存在两个及以上的星时,可以实现拍摄位置定位(双星定位将得到两个可能的拍摄位置解,但通常这两个解相距很远,可舍去不合理的一解)。
如果使用球面距离公式求解星天顶角圆的交集,由于方程复杂性,计算机通常会无法得到数值解。为此,我们运用几何学的知识,将球面距离公式转化为可线性求解的平面几何问题。设两星天文坐标分别为$A(\alpha_i,\delta_i)$,$B(\alpha_j,\delta_j)$,天顶角分别为$\theta_i$,$\theta_j$。从地心到A星的单位矢量可由以下公式表示:
$$\overrightarrow{OA}=(\cos\theta_i\cos\alpha_i,\cos\theta_i\sin\alpha_i,\sin\theta_i)$$
设点K在地球表面,天球投影的坐标为$(\alpha_i+\theta_i,\delta_i)$,则该点也在A星的天顶角圆上。使用下面的坐标转换公式,我们可以将点K转化为直角坐标系下的坐标$(x,y,z)$,即:
$x=\cos(\alpha_i+\theta_i)\cos\delta_i$
$y=\sin(\alpha_i+\theta_i)\cos\delta_i$
$z=\sin\delta_i$
根据点K和$\overrightarrow{OA}$,通过下面的平面点向式方程,我们可以得到天顶角圆所在平面的方程$\mathop{P}_i(x,y,z)=0,即$:
$\mathop{P}_i(x,y,z):\ \overrightarrow{OA}\cdot\overrightarrow{KP} = 0$
同理可得B星的天顶角圆所在平面的方程$\mathop{P}_j(x,y,z)=0$,它们的交线方程可用以下方程表示:
$\mathop{P}_i(x,y,z)=0$
$\mathop{P}_j(x,y,z)=0$
为方便后续计算,\autoref{eq:plane2}可以转化为只与t相关的直线参数方程形式$\bf{L}(t)\to(x,y)$。令$ \left | \bf{L}(t) \right | = 1$,可得到解析解$t_0$,代入\autoref{eq:plane2}进而得到交点坐标$P_0(x,y)$。将其按以下公式转化为球面坐标,即可得到照片拍摄地的地理经纬度$(\alpha,\delta)$,即:
$\alpha=\arctan\frac{y}{x}$
$\delta=\arcsin z$
对于多星情况,我们可以两两求解双星天顶角圆的交点,对所有焦点按欧氏距离远近进行聚类,将其数量最多的聚类簇的点中心作为最终的拍摄地点。
实验
实验设置
我们使用华为nove 8手机实地拍摄了两副夜景,分别命名为夜景一、夜景二,地点都在西北工业大学长安校区内。夜景一包含1轮满月与1颗星,夜景二包含10颗星,两副照片都包含铅垂线分明的建筑物。需注意的是,由于光线干扰,夜景一包含一个红色伪星点,实验时需排除。
除检测满月中心外,其他各项检测超参数均保持一致,以公平地测试我们方法的适用性和抗干扰能力。此外,所有的地理位置数据均由高德地图API提供。
实验结果
图像处理结果
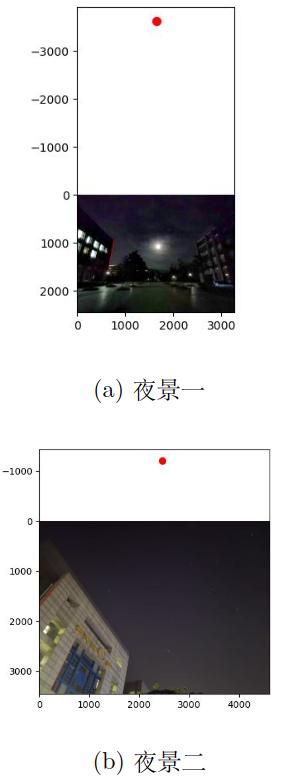

图5展示了我们定位照片的星点中心的效果。可以看到,夜景一的天体1和夜景二的天体2都呈现出不规则的形状,但我们的圆检测方法仍然较好地定位了圆心。夜景一的满月呈现规则的圆形,但其光源特征与星点有所不同,故需调整某些超参,处理得到的结果仍然清楚地表明了我们方法的圆心定位能力的优异。
我们在图4中展示了灭点定位结果。在过滤了各种干扰线后,我们用红色线段标明检测到的直线,用红点标明经迭代优化后的检测到的灭点。结果表明,我们的灭点检测方法能较精确地定位到灭点所在位置,难以用肉眼分辨出误差,几乎能与人工标注相匹敌。
定位精度
| 夜景 | 1 | 2 |
| 实际位置 | 108.76, 34.03 | 108.77, 34.04 |
| 检测位置 | 108.50, 32.72 | 108.48, 34.46 |
| 误差 | 139.3km | 54.3km |
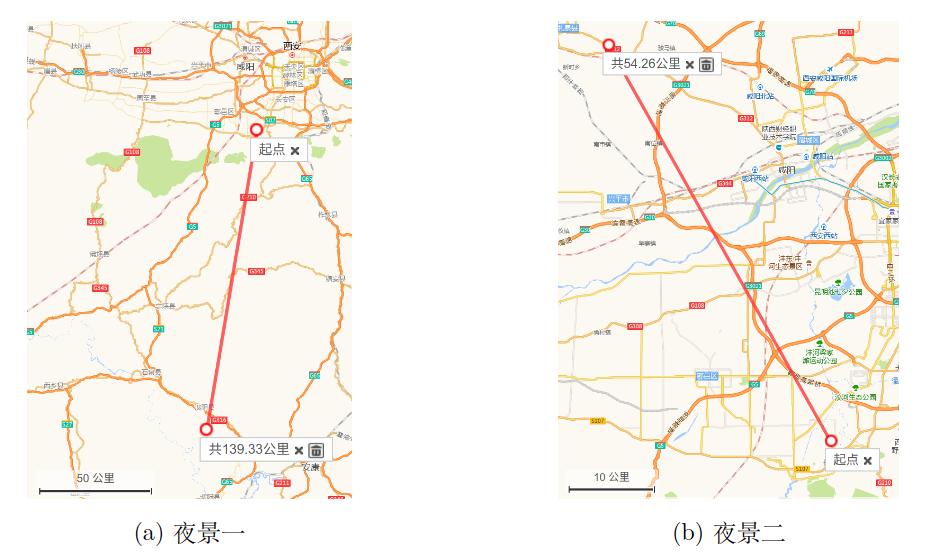
对两张照片的定位精度如表1所示,图6使用地图形式展示了地理位置定位结果。夜景一只有两个天体,误差为139.3km,相当于两个市之间的距离。夜景二有十颗星,误差低至54.3km,仅相当于两个区之间的距离。以上结果表明,我们的方法定位精度较高,对侦查领域有明显的实际应用价值。
消融实验
| 星数 | 2 | 4 | 6 | 8 | 10 |
| 误差/km | 65.8 | 59.9 | 52.9 | 47.9 | 54.3 |
我们通过消融实验,针对夜景二的照片,研究了星数与定位精度的关系,结果如表2所示。可以看到,随着星数的增加,定位精度逐渐提高,但当星数达到6颗时,定位精度已经达到了较高的水平。这表明,我们的方法对星数的要求并不高,即使只有2颗星,也能实现较高的定位精度。
讨论
我们通过数字图像处理的方法,结合天文学和几何学的知识,实现了对单照片的高精度定位。然而,我们的方法仍然存在一些局限性,未来的研究方向包括:
- 我们的方法对星点的要求并不高,但对于星点的分布情况,我们的方法仍然存在一定的局限性。未来的研究可以研究不同位置的星点的坐标信任度和相应权重,进一步提高定位精度。
- 灭点坐标对我们的精度影响较大,未来的研究可以针对夜景特征,引入特别的滤除手段或更多的直线检测灭点检测方法,进一步提高定位精度。
- 我们的方法仍然受限于照片的畸变,而相机的畸变参数在实际应用中很难获取。未来的研究可以通过引入照片畸变自校正方法,来提高定位精度。
结论
我们提出了一种仅基于照片中的星点与拍摄时间的定位方法,无需GPS等信息,适用于军事、侦查等领域。我们选用了鲁棒性较强的霍夫圆变换[1]和LSD算法[2],创造性地提出了基于迭代优化的灭点计算方法,提高了定位的抗干扰能力。我们通过实际测试和灵敏度分析,证明了我们方法的较高定位精度和较强抗干扰能力。
参考文献
[1] D. H. Ballard, “Generalizing the hough transform to detect arbitrary shapes,” Pattern recognition, vol. 13, no. 2, pp. 111– 122, 1981.
[2] R. Grompone von Gioi, J. Jakubowicz, J.M. Morel, and G. Randall, “LSD: a Line Segment Detector,” Image Processing On Line, vol. 2, pp. 35–55, 2012, https://doi. org/10.5201/ipol.2012.gjmr-lsd.
[3] M. Glassman and M. J. Kang, “Intelligence in the internet age: The emergence and evolution of open source intelligence (osint),” Computers in Human Behavior, vol. 28, no. 2, pp. 673–682, 2012.
[4] 鬼蝉, “天文学真的对个人来说,毫无用处吗?- 知乎,” Dec 2023. [Online]. Available: https://www.zhihu.com/question/ 603566190/answer/3313965267
[5] I. Sobel, G. Feldman et al., “A 3×3 isotropic gradient operator for image processing,” a talk at the Stanford Artificial Project in, vol. 1968, pp. 271–272, 1968.
[6] J. M. Prewitt et al., “Object enhancement and extraction,” Picture processing and Psychopictorics, vol. 10, no. 1, pp. 15–19, 1970.
[7] L. G. Roberts, “Machine perception of three-dimensional solids,” Ph.D. dissertation, Massachusetts Institute of Technology, 1963.
[8] J. Canny, “A computational approach to edge detection,” IEEE Transactions on pattern analysis and machine intelligence, no. 6, pp. 679–698, 1986.
[9] D. Marr and E. Hildreth, “Theory of edge detection,” Proceedings of the Royal Society of London. Series B. Biological Sciences, vol. 207, no. 1167, pp. 187–217, 1980.
[10] C. Akinlar and C. Topal, “Edlines: A real- time line segment detector with a false detection control,” Pattern Recognition Letters, vol. 32, no. 13, pp. 1633–1642, 2011.
[11] N. Hamid and N. Khan, “Lsm: perceptually accurate line segment merging,” Journal of Electronic Imaging, vol. 25, no. 6, pp. 061 620–061 620, 2016.
[12] Y. Zhou, H. Qi, and Y. Ma, “End-to-end wireframe parsing,” in ICCV 2019, 2019.
[13] P. Zhao, J. Li, and F. Kang, “Slope surface displacement monitoring based on a photogrammetric system,” Optik, vol. 227, p. 166089, 2021.